Ta prawidłowość, sformułowana przez Roberta Hooke'a (1635-1703) w formie ut tensio sic vis (gdzie naprężenie, tam sila), pozostaje prawdziwa tylko dla niezbyt dużych odkształceń, nie przekraczających tzw. granicy Hooke'a (zwanej też granicą proporcjonalności), i tylko dla niektórych materiałów. Prawo Hooke'a zakłada też, że odkształcenia ciała, w reakcji na działanie sił, następują w sposób natychmiastowy i całkowicie znikają, gdy przyłożone siły przestają działać. Takie uproszczenie jest wystarczające jedynie dla ciał o pomijalnie małej lepkości.
Osiowy stan naprężenia i odkształcenia
Najprostszym przykładem zastosowania prawa Hooke'a jest rozciąganie statyczne prętu Względne wydłużenie takiego pręta jest wprost proporcjonalne do siły przyłożonej do pręta, do jego długości i odwrotnie proporcjonalne do pola przekroju poprzecznego pręta. Współczynnikiem proporcjonalności jest moduł Younga E
gdzie:
- F – siła rozciągająca,
- S – pole przekroju,
- Δl – wydłużenie pręta,
- l – długość początkowa.
W przypadku pręta bądź drutu o stałej średnicy można to wyrazić prościej: wydłużenie względne jest proporcjonalne do działającej siły.
Stosując definicje odkształcenia i naprężenia można powiedzieć, że względne wydłużenie jest proporcjonalne do naprężenia, co można zapisać:
gdzie:
 – odkształcenie względne,
– odkształcenie względne,


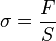 – naprężenie.
– naprężenie.